Mecânica

Escolha o assunto e comece seus estudos!

“Se eu vi mais longe, foi por estar sobre ombros de gigantes.”

Isaac Newton

Cinemática

LISTA 13 – LANÇAMENTO OBLÍQUO

01. (UNESP)

O gol que Pelé não fez

Na copa de 1970, na partida entre Brasil e Tchecoslováquia, Pelé pega a bola um pouco antes do meio de campo, vê o goleiro tcheco adiantado, e arrisca um chute que entrou para a história do futebol brasileiro. No início do lance, a bola parte do solo com velocidade de 108 km/h (30 m/s), e três segundos depois toca novamente o solo atrás da linha de fundo, depois de descrever uma parábola no ar e passar rente à trave, para alívio do assustado goleiro.

Na figura vemos uma simulação do chute de Pelé.

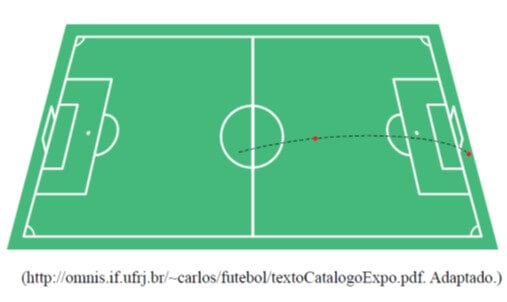
Considerando que o vetor velocidade inicial da bola após o chute de Pelé fazia um ângulo de 30º com a horizontal (sen30º = 0,50 e cos30º = 0,85) e desconsiderando a resistência do ar e a rotação da bola, pode-se afirmar que a distância horizontal entre o ponto de onde a bola partiu do solo depois do chute e o ponto onde ela tocou o solo atrás da linha de fundo era, em metros, um valor mais próximo de

(A) 52,0.

(B) 64,5.

(D) 80,4.

(E) 86,6.

02. (MACKENZIE) Um zagueiro chuta uma bola na direção do atacante de seu time, descrevendo uma trajetória parabólica. Desprezando-se a resistência do ar, um torcedor afirmou:

I. A aceleração da bola é constante no decorrer de todo o movimento.

II. A velocidade da bola na direção horizontal é constante no decorrer de todo o movimento.

III. A velocidade escalar da bola, no ponto de altura máxima, é nula.

A(s) afirmativa(s) correta(s) é (são)

a) somente a I.

b) somente I e III.

c) somente II e III.

d) I, II e III.

e) somente I e II.

03. (FUVEST) O salto que conferiu a medalha de ouro a uma atleta brasileira, na Olimpíada de 2008, está representado no esquema ao lado, reconstruído a partir de fotografias múltiplas. Nessa representação, está indicada, também, em linha tracejada, a trajetória do centro de massa da atleta (CM). Utilizando a escala estabelecida pelo comprimento do salto, de 7,04 m, é possível estimar que o centro de massa da atleta atingiu uma altura máxima de 1,25 m (acima de sua altura inicial), e que isso ocorreu a uma distância de 3,0 m, na horizontal, a partir do início do salto, como indicado na figura.

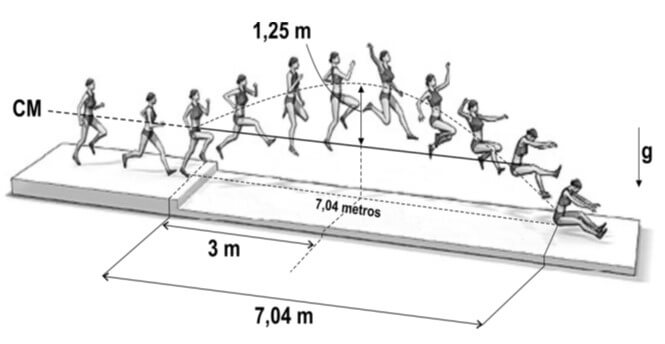
Considerando essas informações, estime:

a) O intervalo de tempo t₁, em s, entre o instante do início do salto e o instante em que o centro de massa da atleta atingiu sua altura máxima.

b) A velocidade horizontal média, V_H, em m/s, da atleta durante o salto.

c) O intervalo de tempo t₂, em s, entre o instante em que a atleta atingiu sua altura máxima e o instante final do salto.

04. (UNIFESP) No campeonato paulista de futebol, um famoso jogador nos presenteou com um lindo gol, no qual, ao correr para receber um lançamento de um dos atacantes, o goleador fenomenal parou a bola no peito do pé e a chutou certeira ao gol. Analisando a jogada pela TV, verifica-se que a bola é chutada pelo armador da jogada a partir do chão com uma velocidade inicial de 20,0 m/s, fazendo um ângulo com a horizontal de 45º para cima. Dados: g = 10,0 m/s² e

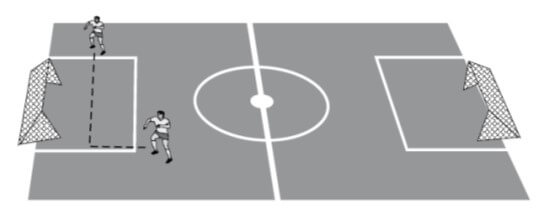
a) Determine a distância horizontal percorrida pela bola entre o seu lançamento até a posição de recebimento pelo artilheiro (goleador fenomenal).

b) No instante do lançamento da bola, o artilheiro estava a 16,0 m de distância da posição em que ele estimou que a bola cairia e, ao perceber o início da jogada, corre para receber a bola. A direção do movimento do artilheiro é perpendicular à trajetória da bola, como mostra a figura. Qual é a velocidade média, em km/h, do artilheiro, para que ele alcance a bola imediatamente antes de ela tocar o gramado?

05. (UNESP) A atleta brasileira Daiane dos Santos teve seu salto “duplo twist carpado” analisado por pesquisadores do Laboratório de Biofísica da Escola de Educação Física da USP. Nesse estudo, verificou-se que, na última parte do salto, o seu centro de massa descreveu uma parábola, que a componente vertical da velocidade inicial da atleta foi de 5,2 m/s e que ela levou 1 s para percorrer uma distância horizontal de 1,3 m até atingir o chão. Adotando g = 10 m/s², determine o ângulo inicial aproximado do salto.

06. (UNIFESP) O atleta húngaro Krisztian Pars conquistou medalha de ouro na olimpíada de Londres no lançamento de martelo. Após girar sobre si próprio, o atleta lança a bola a 0,50 m acima do solo, com velocidade linear inicial que forma um ângulo de 45º com a horizontal. A bola toca o solo após percorrer a distância horizontal de 80 m.

Nas condições descritas do movimento parabólico da bola, considerando a aceleração da gravidade no local igual a 10 m/s², e desprezando-se as perdas de energia mecânica durante o voo da bola, determine, aproximadamente:

a) o módulo da velocidade de lançamento da bola, em m/s.

b) a altura máxima, em metros, atingida pela bola.

07. (ALBERT EINSTEIN) Na modalidade esportiva do salto à distância, o esportista, para fazer o melhor salto, deve atingir a velocidade máxima antes de saltar, aliando-a ao melhor ângulo de entrada no momento do salto que, nessa modalidade, é o 45º. Considere uma situação hipotética em que um atleta, no momento do salto, alcance a velocidade de 43,2 km/h, velocidade próxima do recorde mundial dos 100 metros rasos, que é de 43,9 km/h. Despreze o atrito com o ar enquanto ele está em “voo” e considere o saltador como um ponto material situado em seu centro de gravidade. Nessas condições, qual seria, aproximadamente, a distância alcançada no salto? Adote o módulo da aceleração da gravidade igual a 10 m/s².

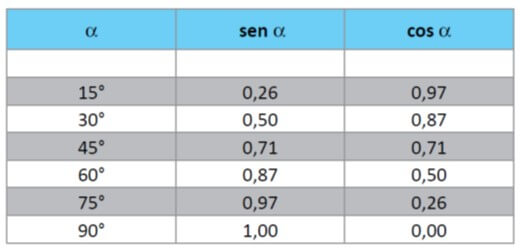
Dados: sen45º = cos45º = 0,7

(A) 7m

(B) 10m

(D) 14m

08. (FAMERP) No interior de um vagão hermeticamente fechado que se move horizontalmente em trajetória retilínea com velocidade 4,0 m/s em relação ao solo, uma pessoa arremessa uma pequena esfera verticalmente para cima, com velocidade 3,0 m/s em relação ao vagão.

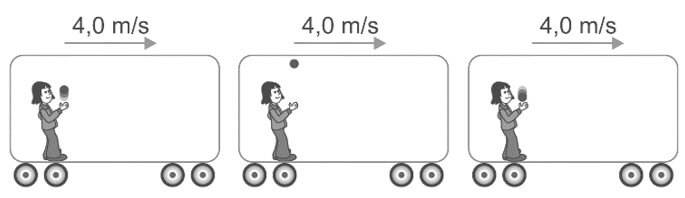
Desprezando o atrito com o ar, os módulos das velocidades da esfera, em relação ao solo, no ponto mais alto de sua trajetória e no instante em que retorna a mão da pessoa são, respectivamente,

a) 4,0 m/s e 3,0 m/s.

b) zero e 5,0 m/s.

c) 4,0 m/s e 5,0 m/s.

d) zero e 3,0 m/s.

e) 5,0 m/s e zero.

09. (SANTA CASA) A partir de uma elevação ao lado de um lago de águas tranquilas, uma criança lançou uma pedra obliquamente para cima com velocidade inicial de módulo 10 m/s e direção que formava um ângulo θ com a horizontal, tal que sen θ = 0,80 e cos θ = 0,60.

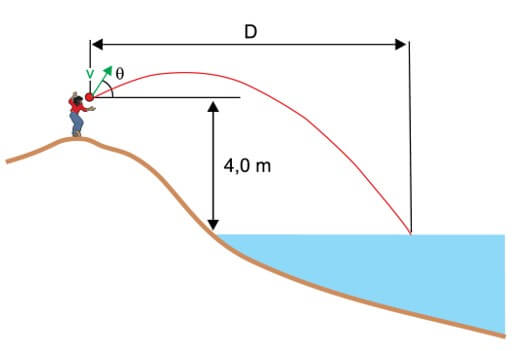
Sabendo que a pedra saiu da mão da criança a uma altura de 4,0 m acima da superfície do lago, considerando g = 10 m/s² e desprezando a resistência do ar, o deslocamento horizontal D da pedra até atingir a superfície do lago foi

(A) 9,6 m.

(B) 11,4 m.

(D) 12,0 m.

(E) 13,6 m.

10. Em um jogo de vôlei, a bola é tocada pelo levantador no ponto A com v₀ = 5 m/s e é atingida pelo atacante no ponto B, 0,5 s depois. De A para B a bola percorre uma trajetória parabólica contida em um plano vertical paralelo ao que contém a rede.

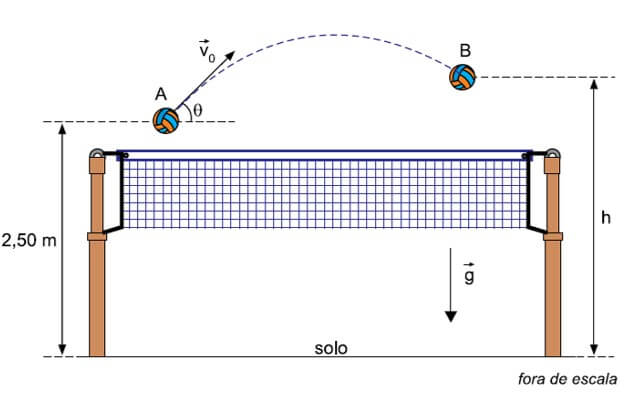
Considerando sen θ = 0,6, cos θ = 0,8, g = 10 m/s² e desprezando a resistência do ar, a altura do ponto B em relação ao solo (h) é igual a

(A) 2,65 m.

(B) 2,85 m.

(D) 2,55 m.

(E) 2,95 m.

Respostas

1- C

2- E

a) t = 0,5 s

b) v = 6 m/s

c) Dt @ 0,67s

a) D = 39,2 m

b) v @ 20 km/h

5- a @ 75º

a) V₀ @ 28 m/s

b) H_max = 20,5 m

a) t = 5 s

b) H = 320 m

c) Dt = 13 s

d) d = 1560 m

7- D

8- C

9- D

10- C